Индукторите могат да си представим обратното на кондензаторите. Основната разлика между кондензатор и индуктор е, че кондензаторът носи защитен диелектрик между своите пластини, който инхибира провеждането на ток през неговите клеми. Тук той действа като отворена верига.
От друга страна, индуктивността на индуктор обикновено е (макар и не винаги) с невероятно ниско или минимално съпротивление. По същество се държи като затворена верига.
Двойственост на кондензаторния индуктор
В електрониката има уникален термин за този тип връзка между два параметъра на верига или части от верига. Елементите от този тип двойка са известни като дуали един на друг . Например, в зависимост от способността за провеждане на ток, отворена верига е двойството на затворена верига.
На същия принцип индуктор е двойник на кондензатор. Двойствеността на индукторите и кондензаторите е много по-дълбока от естествения капацитет за провеждане на ток.
В тази статия сравняваме принципа на работа на индуктор и кондензатор и оценяваме резултатите с изчисления и формули.
Въпреки факта, че индукторите обикновено се виждат рядко в електронните вериги, тъй като днес те са заместени предимно от opamps в активни филтри), другите части, участващи във веригата, изглежда носят известно количество индуктивност.
Самоиндуктивността на клемите на кондензатор или резистор се превръща в голям проблем във високочестотните вериги, което обяснява защо безоловни резистори и кондензатори за повърхностно монтиране се използват толкова често в такива приложения.
Основни кондензаторни уравнения
Основното уравнение за кондензатори е това, с което се определя фарадът:
C = Q / I [уравнение 19]
където C е капацитетът във фарад, Q е зарядът в кулон, а U е pd между плочите във волта.
Чрез уравнение 19, получаваме формула с формата Q = ∫ I dt + c, където c е началният заряд, ако е наличен. След като идентифицирахме Q, можем да определим U от уравнение. 19:
U = 1 / C ∫ I dt + c / C [Уравнение 21]
Важни характеристики на кондензатора могат да бъдат подобни, ако към него се прилага периодичен ток (обикновено ток, който колебае синусоидално), зарядът на кондензатора и напрежението в него също варират синусоидално.
Кривата на заряда или напрежението е отрицателна крива на косинус, или можем да си го представим като крива на синус, която изостава от текущата крива с Пи / 2 работа (90 °).
Основното уравнение, което определя henry, единицата за индуктивност, е
L = NΦ / I [Уравнение 22]
По отношение на единична намотка, самоиндуктивността в henry може да бъде връзката на потока (магнитният поток<1) in weber multiplied by the number of winding N, (because the magnetic flux cuts through each turn), when a unit current passes through it (I = 1 A). An even more handy definition could be extracted from Eq. 22, using Neumann’s equation. This claims that:
U = N (dΦ / dt) [Уравнение 23]
Това, което предполага това уравнение, е фактът, че e.m.f. индуцирана в индуктор е спрямо свързаната скорост на промяна на потока.
Колкото по-бързо варира потока, толкова по-висок е индуцираният e.m.f. Например, когато потокът върху индуктора или намотката се повиши със скорост от 2 mWb s-1, и ако приемем, че бобината има ДВАДЕСЕТ ПЕТ оборота, тогава U = 25x2 = 50V.
Пътят на e.m.f. е такъв, че се противопоставя на вариациите на потока, както е очертано от Закона на Ленц.
Тази истина често се изтъква, като предшестваме дясната страна на уравнението със знак минус, но докато вярваме, че U е задната част e.m.f., знакът може да бъде премахнат.
Диференциали
Терминът dΦ / dt в уравнение 23 показва това, което научихме като скорост на промяна на потока. Фразата се нарича диференциал на Φ по отношение на t и цял клон на аритметиката е посветен на работата с този вид изрази. Фразата има формата на единично число (dΦ), разделено на още едно количество (dt).
Диференциалите се използват за свързване на множество набори пропорции: dy / dx, например, корелира променливи x и y. Когато графиката се начертае, като се използват стойности на x през хоризонталната ос и стойности на y през вертикалната ос, dy / dx означава колко стръмен е наклонът или градиентът на графиката.
Ако U е напрежението на FET порта-източник, където T е съответният източен ток, тогава dI / dU означава количеството, с което се променя за дадени промени в U. Алтернативно можем да кажем, че dI / dU е транспроводимостта. Докато обсъждаме индукторите, dΦ / dt може да бъде скоростта на промяна на потока с времето.
Изчисляването на диференциал може да се разглежда като обратна процедура на интегриране. В тази статия няма достатъчно място за разглеждане на теорията на диференциацията, въпреки това ще определим таблица на често използваните величини заедно с техните диференциали.
Стандартни диференциали

Горната таблица работи, като използва I и t като фактори вместо рутинните x и y. Така че неговите детайли са конкретно свързани с електрониката.
Като пример, като се има предвид, че I = 3t +2, начинът, по който се отклонявам по отношение на времето, може да се визуализира в графиката на фиг. 38. За да намерим скоростта на промяна на I във всеки момент, ние изчисляваме dI / dt, чрез позовавайки се на таблицата.

Първият елемент във функцията е 3t или, за да го форматирате като първи ред на таблицата, 3t1. Ако n = 1, диференциалът е 3t1-1= 3t0.
Тъй като t0= 1, диференциалът е 3.
Второто количество е 2, което може да се изрази като 2t0.
Това променя n = 0 и величината на диференциала е нула. Диференциалът на константата винаги ще бъде нула. Получавайки и двете в комбинация, имаме:
dI / dt = 3
В тази илюстрация диференциалът не включва t, което означава, че диференциалът не зависи от времето.
Казано по-просто, наклонът или градиентът на кривата на фиг. 38 е 3 непрекъснато през цялото време. Фигура 39 по-долу показва кривата за различна функция, I = 4 sin 1.5t.

С позоваване на таблицата, α = 1,5 и b = 0 в тази функция. Таблицата показва, dl / dt = 4x1.5cos1.5t = 6cos 1.5t.
Това ни информира за моментната скорост на промяна на I. Например, при t = 0,4, dI / dt = 6cos0,6 = 4,95. Това може да се забележи на фиг. 39, в която кривата за 6 cos0.6t включва стойността 4.95, когато t = 0.4.
Можем също така да забележим, че наклонът на кривата 4sin1.5t е 4,95, когато t = 0,4, както е показано от допирателната към кривата в тази точка (по отношение на различните скали по двете оси).
Когато t = π / 3, точка, когато токът е най-висок и постоянен, в този случай dI / dt = 6cos (1,5xπ / 3): 0, съответстваща на нулева промяна на тока.
Напротив, когато t = 2π / 3 и токът превключва на възможно най-високо ниво от положително на отрицателно, dI / dt = 6cosπ = -6, виждаме най-високата му отрицателна стойност, показваща голямо намаляване на тока.
Простото предимство на диференциалите е, че те ни позволяват да определим скоростта на промяна за функции, които са много по-сложни в сравнение с I = 4sin 1.5t, и без да се налага да начертаваме кривите.
Обратно към изчисленията
Чрез реорганизация на условията в уравнение 22 получаваме:
Φ = (L / N) I [Уравнение 24]
Където L и N имат постоянни размери, но Φ и I може да има стойност по отношение на времето.
Диференцирането на двете страни на уравнението по отношение на времето дава:
dΦ / dt = (L / N) (dI / dt) [Уравнение 25]
Обединяването на това уравнение с уравнение 23 дава:
U = N (L / N) (dI / dt) = L (dI / dt) [Уравнение 26]
Това е друг начин за изразяване на Хенри . Можем да кажем, че намотка със самоиндуктивност 1 H, промяна на тока от 1 A s-1генерира обратно e.m.f. от 1 V. Дадена функция, която определя как даден ток се променя във времето, уравнение 26 ни помага изчислете гърба e.m.f. на индуктор във всеки един момент.
Следват няколко примера.
A) I = 3 (постоянен ток от 3 A) dl / dt = 0. Не можете да намерите промяна на тока, следователно задният e.m.f. е нула.
B) I = 2t (ток на рампа) dI / dt = 2 A s-1. С бобина, носеща L = 0,25 H, гърбът e.m.f. ще бъде постоянна при 0,25x2 = 0,5 V.
C) I = 4sin1.5t (синусоидалният ток, даден на предишната илюстрация dl / dt = 6cos 1.5t. При дадена намотка с L = 0.1 H, моментната задна едс е 0.6cos1.5t. Задната emf следва диференциалната крива на фиг. 39, но с амплитуда 0,6 V, а не 6 A.
Разбиране на „дуалите“
Следните две уравнения означават уравнението съответно на кондензатор и индуктор:

Помага ни да определим нивото на напрежение, произведено в компонента чрез ток, вариращ във времето според конкретна функция.
Нека да оценим резултата, получен от разграничаване L и H страните на уравнение 21 по отношение на времето.
dU / dt = (1 / C) I
Както знаем, че диференциацията е обратна на интеграцията, диференциацията на ∫I dt обръща интеграцията, като резултатът е само I.
Диференцирането на c / C дава нула и пренареждането на условията води до следното:
I = C.dU / dt [Уравнение 27]
Това ни позволява да знаем посоката на тока, независимо дали той отива към кондензатора или излиза от него, в отговор на напрежение, вариращо в зависимост от дадена функция.
Интересното е, че горното кондензаторно уравнение на тока изглежда подобно на уравнението на напрежението (26) на индуктор, който показва капацитет, индуктивност двойственост.
По същия начин токовата и потенциалната разлика (pd) или скоростта на промяна на тока и pd могат да бъдат двойни, когато се прилагат към кондензатори и индуктори.
Нека сега интегрираме уравнение 26 по отношение на времето, за да завършим уравнението:
∫ U dt + c = LI
Интегралът на dI / dt е = I, ние пренареждаме изразите, за да получим:
I = 1 / L∫ U dt + e / L
Това отново изглежда доста подобно на уравнение 21, което допълнително доказва двойствения характер на капацитета и индуктивността и техния pd и ток.
Към момента имаме набор от четири уравнения, които могат да се използват за решаване на проблеми, свързани с кондензатор и индуктор.
За пример може да се приложи уравнение 27 за решаване на проблема, както този:
Проблем: Импулсът на напрежение, приложен през 100uF, създава крива, както е показано на фигурата по-долу.

Това може да се определи, като се използва следната функция на парчета.

Изчислете тока, който се движи през кондензатора, и начертайте съответните графики.
Решение:
За първия етап прилагаме уравнение 27
I = C (dU / dt) = 0
За втория случай, когато U може да се покачва с постоянна скорост:
I = C (dU / dt) = 3C = 300μA
Това показва постоянен ток на зареждане.
За третия етап, когато U пада експоненциално:

Това показва ток, изтичащ от кондензатора с експоненциално намаляваща скорост.
Фазова връзка

На фигурата на абобето върху индуктор се прилага променлив pd. Този pd във всеки един момент може да бъде изразен като:

Където Uo е пиковата стойност на pd. Ако анализираме веригата под формата на цикъл и приложим закона на напрежението на Kirchhoff по посока на часовниковата стрелка, ще получим:

Тъй като обаче токът е синусоидален тук, членовете в скобата трябва да имат стойността, равна на пиковия ток Io, следователно най-накрая получаваме:

Ако сравним уравнението 29 и уравнение 30, ще установим, че токът I и напрежението U имат еднаква честота и аз изоставам от U с π / 2.
Резултантните криви могат да бъдат изследвания в следната диаграма:

° С
Това показва контрастната връзка между кондензатора и индуктора. За индуктивния ток изостава потенциалната разлика с π / 2, докато за кондензатор токът води pd. Това още веднъж демонстрира двойствената природа на двата компонента.
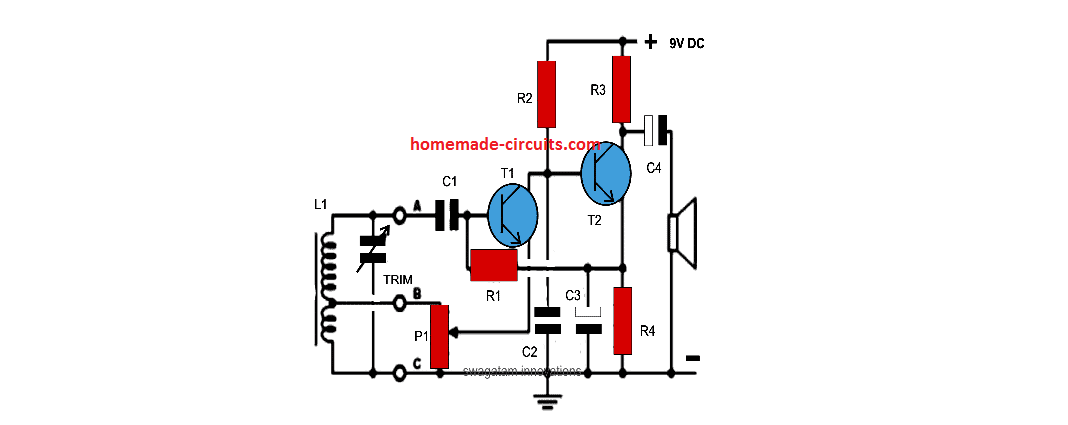
Предишна: Предавателна верига 27 MHz - обхват 10 км Напред: H-Bridge Bootstrapping