В компютрите трябва да преобразуваме двоичното в сиво и сивото в двоично. Преобразуването на това може да стане чрез използване на две правила, а именно преобразуване в двоично в сиво и преобразуване в сиво в двоично. При първото преобразуване MSB на сивия код е постоянно еквивалентен на MSB на двоичния код. Допълнителни битове от изхода на сивия код могат да получат, използвайки концепцията за логическа порта EX-OR към двоичните кодове в настоящия индекс, както и по-ранния индекс. Тук MSB не е нищо друго освен най-значимият бит. При първото преобразуване MSB на двоичния код е постоянно еквивалентен на MSB на конкретния двоичен код. Допълнителни битове от изхода на двоичния код могат да получат с помощта на EX-OR логическа порта концепция чрез проверка на сивите кодове при настоящия индекс. Ако настоящият бит на сивия код е нула, тогава след това копирайте по-ранен двоичен код, както и копирайте обратното на по-ранен битарен двоичен код. Тази статия разглежда общ преглед на преобразувателите на код, който включва преобразувател на двоичен в сив код, както и конвертор в сив в двоичен код.
Какво е двоичен код?
В цифровите компютри кодът, който се използва въз основа на двоична бройна система, е известен като двоичен код. Има две възможни състояния като ВКЛ. И ИЗКЛ., Които са представени чрез 0 и 1. Цифровата система използва 10 цифри, където всяка позиция на цифра означава степента на 10. В бинарната система всяка позиция на цифра представлява степен на 2.
Сигналът с двоичен код включва поредица от електрически импулси, които означават символи, числа и операции, които трябва да бъдат изпълнени. Устройство с часовник се използва за предаване на нормални импулси, както и компоненти като транзистори, включване / изключване за протичане, в противен случай блокира сигналите. В двоичен код всеки десетичен брой в диапазона от 0 до 9 може да бъде означен чрез набор от 4-бинарни бита / цифри. Основните 4 аритметични операции като събиране, изваждане, умножение и деление могат да бъдат намалени до комбинации от основни булеви алгебрични функции върху двоични числа.
Какво представлява Сивият код?
Сивият код или RBC (отразен двоичен код) или цикличният код е поредица от двоични бройни системи. Основната причина да се извика този отразен двоичен код е, че първоначалните N / 2 стойности са в обратен ред в сравнение с последните N / 2 стойности. При този вид код двете последователни стойности се променят чрез един бит двоични цифри. Тези кодове се използват главно в общата поредица от двоични числа, генерирани от хардуер.
Двоичните числа могат да причинят грешки, след като преходът бъде извършен от едно число към поредно. Този тип код основно решава този проблем, като променя само един бит, след като е извършена промяната между числата.
Този вид код е изключително лек и не зависи от цифровата стойност, посочена в цялата позиция. Този вид код също се нарича цикличен променлив код, тъй като промяната на единична стойност до нейната последователна стойност съдържа промяна само на един бит.
Това е най-популярното за единичните кодове за разстояние, но не е подходящо за аритметични функции. Приложенията на сивия код включват аналогови към цифрови преобразуватели и цифрова комуникация за корекция на грешки. Първо, сивият код не е лесен за разбиране, но се превръща в много по-лесен за разпознаване.
Преобразувател на двоичен в сив код
Двоичният код е много просто представяне на данни, използвайки две стойности като 0 и 1 и се използва главно в света на компютъра. Двоичният код може да бъде висока (1) или ниска (0) стойност или дори да промени стойността. Сивият код или отразеният двоичен код изчислява естеството на двоичния код, който е подреден с индикатори за включване и изключване, обикновено обозначени с единици и нули. Тези кодове се използват за разглеждане на яснотата, както и промяна на грешки в двоичен файл комуникации .
Преобразуването на двоичен в сив код може да се извърши с помощта на логическа схема . Сивият код е нетеглен код, тъй като няма определена тежест за позицията на бита. N-битов код може да бъде получен чрез възпроизвеждане на n-1 битов код на ос, следваща редовете от 2n-1, както и поставяне на най-значимия бит 0 над оста с най-значимия бит 1 под оста. Генерирането на сив код стъпка по стъпка е показано по-долу.

Логическа схема за преобразуване на двоичен в сив код
Този метод използва Ex-OR порта за изпълнение сред двоичните битове. Следващият най-добър пример ще бъде много полезен за познаване на преобразуването на двоично в сиво. В този метод на преобразуване свалете MSB бита на настоящото двоично число, тъй като основният бит или MSB битът на сивия код е подобен на двоичния номер.
За да получите правите сиво кодирани битове за генериране на съответната сива кодирана цифра за дадените двоични цифри, добавете основната цифра или MSB цифрата на двоично число към втората цифра и запишете продукта до основния бит сив код добавете следващия двоичен бит към третия бит, след което запишете продукта до 2ndмалко сив код. По същия начин следвайте тази процедура до крайния двоичен бит, както и запишете резултатите в зависимост от EX-OR логическа операция за генериране на съответната сиво кодирана двоична цифра.
Пример за конвертор на двоичен в сив код
Нека приемем, че цифрите на двоичния код са bo, b1, b2, b3, докато конкретният сив код може да бъде постигнат въз основа на следната концепция.

Пример за преобразуване на код
От горната операция накрая можем да получим сивите стойности като g3 = b3, g2 = b3 XOR b2, g1 = b2 XOR b1, g0 = b1 XOR b0.

Пример за преобразуване
Например вземете двоичната стойност b3, b2, b1, b0 = 1101 и намерете сивия код g3, g2, g1, g0 въз основа на горната концепция
g3=b3=1
g2 = b3 XOR b2 = 1 XOR 1 = 0
g1 = b2 XOR b1 = 1 XOR 0 = 1
g0 = b1 XOR b0 = 0 XOR 1 = 1
Крайният сив код за стойността на двоичен 1101 е 1011
Таблица за преобразуване на двоичен в сив код
Десетично число | Двоичен код | Сив код |
0 | 0000 | 0000 |
| 1 | 0001 | 0001 |
две | 0010 | 0011 |
3 | 0011 | 0010 |
4 | 0100 | 0110 |
| 5 | 0101 | 0111 |
6 | 0110 | 0101 |
| 7 | 0111 | 0100 |
8 | 1000 | 1100 |
9 | 1001 | 1101 |
| 10 | 1010 | 1111 |
единадесет | 1011 | 1110 |
12 | 1100 | 1010 |
13 | 1101 | 1011 |
| 14. | 1110 | 1001 |
| петнадесет | 1111 | 1000 |
VHDL код за преобразуване в двоичен в сив код е дадено по-долу.
БИБЛИОТЕКА ieee
ИЗПОЛЗВАЙТЕ ieee.std_logic_1164.ALL
обект bin2gray е
порт (bin: в std_logic_vector (3 в центъра 0) - двоичен вход
G: излиза std_logic_vector (3 в центъра 0) - изход на сив код
)
край bin2gray
архитектура gate_level на bin2gray е
започнете
–Xor порти.
G (3)<= bin(3)
G (2)<= bin(3) xor bin(2)
G (1)<= bin(2) xor bin(1)
G (0)<= bin(1) xor bin(0)
край
Предимства
The предимства на двоичния код включват следното.
- Основната полза от използването на двоичен код е, че той просто се обозначава чрез електронни устройства
- Двоичните данни също са много лесни за съхранение.
- Много лесно за означаване и контрол по електронен и механичен начин.
- Несъответствието между представянията на символи може да бъде увеличено, така че възможността за грешка може да бъде намалена.
The недостатъци на двоичния код включват следното.
- Необходимият брой символи може да бъде увеличен, за да обозначи определен брой системи за стойност на общата позиция.
- Хората не могат да ги четат изключително ефективно поради тяхната дължина и и използването на основни десет числа по подразбиране
- Той използва много цифри, за да обозначи всяко логическо число
Приложения
Приложенията на двоичен код включват следното.
- Двоичните кодове се използват в телекомуникациите, както и за изчисления за различни техники на кодиране на данни като символни низове до битови низове. Ширината, използвана от тези методи, е фиксирана в противен случай низове с променлива ширина.
- Това се използва в компютърните езици, както и в програмирането, тъй като компютърните езици зависят главно от двуцифрени бройни системи.
Конвертор на сиво в двоичен код
Този метод на преобразуване в сиво в двоично също използва работната концепция на логическата порта EX-OR сред битовете на сивото, както и бинарните битове. Следващият пример с процедура стъпка по стъпка може да ви помогне да разберете концепцията за преобразуване на сивия код в двоичен код.
За да промените сивия на двоичен код, свалете MSB цифрата на сивия код, тъй като основната цифра или MSB на сивия код е подобна на двоичната цифра.
За да получи следващия прав двоичен бит, той използва операцията XOR сред основния бит или MSB бита двоичен към следващия бит на сивия код.

Логическа схема за преобразуване на сиво в двоичен код
По същия начин, за да получи третия прав двоичен бит, той използва операцията XOR сред втория бит или бита на MSB двоичен към третия бит MSD на сивия код и така нататък.
Пример за конвертор на сиво в двоичен код
Нека приемем Сив код цифри g3, g2, g1, g0, докато конкретните двоични кодови цифри са bo, b1, b2, b3, могат да бъдат получени въз основа на следната концепция.

Пример за преобразуване
От горната операция накрая можем да получим двоичните стойности като b3 = g3, b2 = b3 XOR g2, b1 = b2 XOR g1, b0 = b1 XOR g0.

Пример за преобразуване на код
Например вземете сивата стойност g3, g2, g1, g0 = 0011 и намерете двоичния код b3, b2, b1, b0 въз основа на горната концепция
b3=g3=0
b2 = b3 XOR g2 = 0 XOR 0 = 0
b1 = b2 XOR g1 = 0 XOR 1 = 1
b0 = b1 XOR g0 = 1 XOR 1 = 0
Крайният двоичен код за стойността на сивото 0011 е 0010
Таблица за преобразуване на сиво в двоичен код
| Десетично число | Сив код | Двоичен код |
0 | 0000 | 0000 |
1 | 0001 | 0001 |
| две | 0010 | 0010 |
3 | 0011 | 0011 |
4 | 0110 | 0100 |
| 5 | 0111 | 0101 |
6 | 0101 | 0110 |
| 7 | 0100 | 0111 |
8 | 1100 | 1000 |
| 9 | 1101 | 1001 |
10 | 1111 | 1010 |
| единадесет | 1110 | 1011 |
12 | 1010 | 1100 |
| 13 | 1011 | 1101 |
14. | 1001 | 1110 |
| петнадесет | 1000 | 1111 |
Предимства
The предимства на сивия код включват следното.
- Логическата схема може да бъде намалена
- Използва се при пресичане на часовниковия домейн
- Използва се за минимизиране на грешката при промяна на сигналите от аналогов на цифров
- След като се използва в рамките на генетичните алгоритми, появата на стена на Hamming може да бъде намалена.
Недостатъци
Недостатъците на сивия код включват следното.
- Не е подходящо за аритметични функции
- Приложим за няколко точни приложения
Приложения
Приложенията на сивия код включват следното.
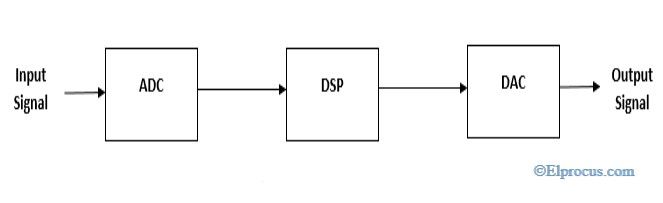
- Използва се в аналогово-цифрови преобразуватели
- При цифрова комуникация за коригиране на грешка
- Намалява грешките, докато променя сигналите от аналогови на цифрови.
- Математически пъзели
- Минимизиране на булева схема
- Използва се за комуникация между два часовникови домейна
- Генетични алгоритми
- Датчици за позиция
VHDL код за сив код в двоично преобразуване е дадено по-долу.
БИБЛИОТЕКА ieee
ИЗПОЛЗВАЙТЕ ieee.std_logic_1164.ALL
субектът Gray2bin е
порт (G: в std_logic_vector (3 в центъра 0) - въвеждане на сив код
bin: out std_logic_vector (3 downto 0) - двоичен изход
)
край сив2бин
архитектура gate_level на gray2bin е
започнете
–Xor порти.
сутринта (3)<= G(3)
сутринта (2)<= G(3) xor G(2)
сутринта (1)<= G(3) xor G(2) xor G(1)
сутринта (0)<= G(3) xor G(2) xor G(1) xor G(0)
край
3-битов конвертор на двоичен в сив код
Да приемем двоичните цифри в 3-битово двоично число като b0, b1, b2, където битът ‘b2’ е MSB (най-значимият бит), а битът ‘b0’ е LSB (най-малко значимият бит) на двоичен файл. Цифрите на кода на Грей са g0, g1, g2, където цифрата ‘g2’ е MSB (най-значимият бит), докато цифрата ‘g0’ е LSB (най-малко значимият бит) на кода на Грей.
| Двоичен код - b2, b1, b0 | Сив код - g2, g1, g0 |
000 | 000 |
| 001 | 001 |
010 | 011 |
| 011 | 010 |
100 | 110 |
| 101 | 111 |
| 110 | 101 |
| 111 | 100 |
По този начин, булевият израз може да бъде решен за преобразувател на двоичен в сив код с помощта на k-map, можем да получим g2 = b2, g1 = b1⊕ b2 & g0 = b0 ⊕ b1. По същия начин можем да променим n-битово двоично число (bnb (n-1) ... b2 b1 b0) в сив код (gng (n-1) ... g2 g1 g0).
За LSB (най-малко значителен бит)
g0 = b0⊕b1
g1 = b1⊕b2
g2 = b1⊕b2
g (n-1) = b (n-1) ⊕ bn, gn = bn.
Например, конвертирайте 111010 двоични числа в сив код.
Въз основа на горния алгоритъм,
g0 = b0 ⊕ b1 => 0 ⊕ 1 = 1
g1 = b1 ⊕ b2 = 1 ⊕ 0 = 1
g2 = b2 ⊕ b3 = 0 ⊕1 = 1
g3 = b3 ⊕ b4 = 1⊕1 = 0
g4 = b4 ⊕ b5 = 1 ⊕ 1 = 0
g5 = b5 = 1 = 1
Така че преобразуването на двоичен в сив код ще бъде - 100111.
Преобразувател на двоичен в сив код с помощта на IC 7486
Преобразуването на двоично в сиво и сиво в двоично може да се извърши с помощта на IC7486. Необходимите компоненти за това са макет, свързващи проводници, светодиоди, резистори, XOR (IC7486), бутони и батерия за захранването.
Пакетът на IC7486 включва основно четири логически порта XOR, където щифтове 7 и 14 ще осигурят захранване за всички логически порта. O / ps на единична XOR порта е свързана към входа на другата логическа порта в рамките на същия или друг чип, докато те споделят подобен заземителен терминал.
По този начин става въпрос за конвертор на двоичен в сив код и конвертор в сив в двоичен код. От горната информация накрая можем да заключим, че тези преобразуватели играят съществена роля при извършване на различни операции на цифрова електроника както и комуникации между различни бройни системи. Примерите за преобразувател на код, които обсъдихме по-горе, могат да бъдат полезни за разбирането на концепцията за това как да се правят тези изчисления. Ето въпрос към вас, какви са приложенията на сивите кодове?