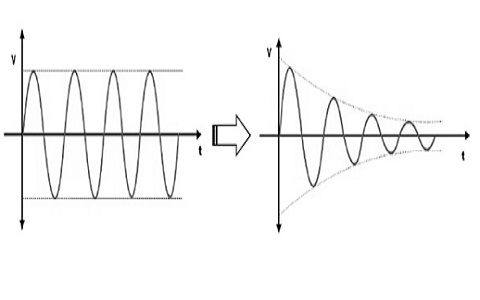
Имаше ера, в която, докато правеше телефонно обаждане на отдалечени места, човек трябваше да постави устата си много близо до предавателя, да говори много бавно и много силно, така че съобщението да може да бъде чуто ясно от човека в другия край. Днес дори можем да правим видео разговори по целия свят с висококачествени резолюции. Тайната на такова огромно развитие на технологиите се крие в Електрически филтър теория и Теория на преносната линия . Електрическите филтри са вериги, които преминават само избрана честотна лента, като същевременно затихват други нежелани честоти. Един от тези филтри е Високочестотен филтър .
Какво е високочестотен филтър?
Дефиницията на високочестотен филтър е филтър, който пропуска само онези сигнали, чиито честоти са по-високи от граничните честоти, като по този начин затихват сигналите от по-ниски честоти. Стойността на граничната честота зависи от конструкцията на филтъра.
Високочестотна верига на филтъра
Основният високочестотен филтър е изграден чрез последователна връзка на кондензатор и резистор . Докато входният сигнал се прилага към кондензатора , изходът се изтегля през резистора .

Високочестотна верига на филтъра
При тази схема на кондензатора кондензаторът има високо съпротивление при по-ниски честоти, така че действа като отворена верига към нискочестотните входни сигнали, докато достигне граничната честота ‘fc’. Филтърът отслабва всички сигнали под нивото на граничната честота. При честоти над прекъснатата честота реактивността на кондензатора става ниска и действа като късо съединение на тези честоти, като по този начин им позволява да преминат директно към изхода.
Пасивен RC високочестотен филтър
Показаният по-горе високочестотен филтър е известен също като Пасивен RC високочестотен филтър тъй като веригата е изградена само с използване пасивни елементи . Не е необходимо да се прилага външно захранване за работа на филтъра. Тук кондензаторът е реактивният елемент и изходът се изтегля през резистора.
Характеристики на високочестотния филтър
Когато говорим за гранична честота ние се позоваваме на точката в честотна характеристика на филтъра където коефициентът на усилване е равен на 50% пиковото усилване на сигнала, т.е. 3dB на пиковото усилване. При високочестотния филтър печалбата се увеличава с увеличаване на честотите.

Крива на честотата на високочестотния филтър
Тази гранична честота fc зависи от стойностите на R и C на веригата. Тук Времева константа τ = RC, граничната честота е обратно пропорционална на времевата константа.
Честота на отрязване = 1 / 2πRC
Печалбата на веригата се дава от AV = Vout / Vin
.i.e. AV = (Vout) / (V in) = R / √ (Rдве+ Xcдве) = R / Z
При ниска честота f: Xc → ∞, Vout = 0
При високочестотна f: Xc → 0, Vout = Vin
Честотен отговор на високочестотния филтър или график на Bode на високочестотния филтър
Във високочестотния филтър всички честоти, лежащи под граничната честота ‘fc’, са отслабени. В тази отсечена честотна точка получаваме -3dB усилване и в този момент реактивното съпротивление на кондензатора и резистора ще бъде еднакво, т.е. R = Xc. Печалбата се изчислява като
Коефициент на усилване (dB) = 20 log (Vout / Vin)
Наклонът на кривата на високочестотния филтър е +20 d B / десетилетие, т.е. след преминаване на нивото на граничната честота, изходният отклик на веригата се увеличава от 0 до Vin със скорост от +20 dB на десетилетие, което е 6 dB увеличение на октава.

Честотен отговор на високочестотния филтър
Областта от началната точка до граничната точка на честотата е известна като стоп лента, тъй като не е разрешено преминаване на честоти. Областта отгоре на граничната точка на границата. т.е. -3 dB точка е известна като лента за преминаване . При гранична честота амплитудата на изходното напрежение на точката ще бъде 70,7% от входното напрежение.
Тук честотна лента на филтъра обозначава стойността на честотата, от която е позволено да преминават сигнали. Например, ако честотната лента на високочестотния филтър е дадена като 50 kHz, това означава, че е разрешено да преминават само честоти от 50 kHz до безкрайност.
Фазовият ъгъл на изходния сигнал е +450 при граничната честота. Формулата за изчисляване на фазовото отместване на високочестотния филтър е
∅ = арктан (1 / 2πfRC)

Крива на фазово изместване
На практика приложението на изхода на филтъра не се простира до безкрайност. Електрическата характеристика на филтърните елементи прилага ограничението към реакцията на филтъра. Чрез правилен подбор на компонентите на филтъра можем да регулираме обхвата на честотите, които трябва да бъдат затихвани, обхвата, който трябва да бъде предаден и т.н. ...
Високочестотен филтър, използващ Op-Amp
В този високочестотен филтър, заедно с пасивни филтриращи елементи, добавяме Op-amp към веригата. Вместо да получи безкраен изходен отговор, тук изходният отговор е ограничен от отворен цикъл характеристики на Op-усилвателя . Следователно този филтър действа като a лентов филтър с пресечна честота, която се определя от честотната лента и характеристиките на усилване на Op-amp.

Високочестотен филтър, използващ Op-Amp
Усилването на напрежението с отворен контур на Op-amp действа като ограничение на честотната лента на усилвателя . Коефициентът на усилване на усилвателя намалява до 0 dB с увеличаването на входната честота. Отговорът на веригата е подобен на пасивния високочестотен филтър, но тук усилването на Op-усилвателя усилва амплитудата на изходния сигнал.
The печалба на филтъра използване на неинвертиращ Op-amp се дава от:
AV = Vout / Vin = (Изкл. (F / fc)) / √ (1+ (f / fc) ^ 2)
където Af е усилването на лентата на пропускане на филтъра = 1+ (R2) / R1
f е честотата на входния сигнал в Hz
fc е граничната честота
Когато ниска толерантност резистори и кондензатори се използват тези High Pass Active филтри осигуряват добра точност и производителност.
Активен високочестотен филтър
Високочестотен филтър, използващ Op-amp е известен също като активен високочестотен филтър тъй като заедно с пасивните елементи кондензатор и резистор е активен елемент Op-amp се използва във веригата . Използвайки този активен елемент, ние можем да контролираме граничната честота и обхвата на реакцията на изхода на филтъра.
Високочестотен филтър от втори ред
Филтърните вериги, които видяхме досега, се считат за високочестотни филтри от първи ред. При високочестотен филтър от втори ред, допълнителен блок от RC мрежа се добавя към високочестотен филтър от първи ред на входния път.
Високочестотен филтър от втори ред
The честотна характеристика на високочестотен филтър от втори ред е подобен на високочестотния филтър от първи ред. Но при втория ред филтър за спиране на високочестотния филтър ще бъде два пъти по-висок от филтъра от първи ред при 40dB / Decade. Филтрите от по-висок ред могат да се формират чрез каскадни филтри от първи и втори ред. Въпреки че няма ограничение за реда, размерът на филтъра се увеличава заедно с техния ред и влошаване на точността. Ако във филтър от по-висок ред R1 = R2 = R3 и т.н ... и C1 = C2 = C3 = и т.н ..., тогава граничната честота ще бъде същата, независимо от реда на филтъра.

Високочестотен филтър от втори ред
Честотата на прекъсване на втория ред High Pass Active филтър може да бъде дадена като
fc = 1 / (2π√ (R3 R4 C1 C2))
Функция за прехвърляне на високочестотен филтър
Тъй като импедансът на кондензатора се променя често, електронните филтри имат честотно зависим отговор.
Комплексният импеданс на кондензатор е даден като Zc = 1 / sC
Където s = σ + jω, ω е ъгловата честота в радиани в секунда
Предавателната функция на верига може да бъде намерена с помощта на стандартни техники за анализ на вериги като Законът на Ом , Законите на Kirchhoff , Суперпозиция и т.н. Основната форма на трансферна функция се дава от уравнението
H (s) = (am s ^ m + a (m-1) s ^ (m-1) + ⋯ + a0) / (bn s ^ n + b (n-1) s ^ (n-1) + ⋯ + b0)
The ред на филтъра е известен със степента на знаменателя. Поляци и нули от веригата се извличат чрез решаване на корени на уравнението. Функцията може да има реални или сложни корени. Начинът, по който тези корени са нанесени на s равнина, където σ се означава с хоризонталната ос, а ω се обозначава с вертикалната ос, разкрива много информация за веригата. За високочестотен филтър нула е разположена в началото.
H (jω) = Vout / Vin = (-Z2 (jω)) / (Z1 (jω))
= - R2 / (R1 + 1 / jωC)
= -R2 / R1 (1 / (1+ 1 / (jωR1 C))
Тук H (∞) = R2 / R1, печалба при ω → ∞
τ = R1 C и ωc = 1 / (τ), т.е. ωc = 1 / (R1C) е граничната честота
По този начин предавателната функция на високочестотния филтър се дава от H (jω) = - H (∞) (1 / (1+ 1 / jωτ))
= - H (∞) (1 / (1- (jωc) / ω))
Когато входната честота е ниска, тогава Z1 (jω) е голяма, следователно изходната реакция е ниска.
H (jω) = (- H (∞)) / √ (1+ (ωc / ω) ^ 2) = 0, когато ω = 0 H (∞) / √2, когато ω = ω_c
и H (∞), когато ω = ∞. Тук отрицателният знак показва фазово изместване.
Когато R1 = R2, s = jω и H (0) = 1
И така, трансферната функция на високочестотния филтър H (jω) = jω / (jω + ω_c)
Масло на стойност високочестотен филтър
Освен че отхвърля нежеланите честоти, идеалният филтър трябва да има и еднаква чувствителност за желаните честоти. Такъв идеален филтър е непрактичен. Но Стивън Бътър, който си струва в своята статия „За теорията на филтърните усилватели“, показва, че този тип филтри могат да бъдат постигнати чрез увеличаване на броя на филтриращите елементи с правилна величина.
Масло на стойност филтър е проектиран по такъв начин, че дава плоска честотна характеристика в честотната лента на филтъра и намалява към нула в ограничителната лента. Основен прототип на Масло на стойност филтър е нискочестотен дизайн но чрез модификации висок проход и лентови филтри може да се проектира.
Както видяхме по-горе, за първи ред филтър за високочестотен филтър печалбата е H (jω) = jω / (jω + ω_c)
За n такива филтри в серия H (jω) = (jω / (jω + ω_c)) ^ n което при решаване е равно на

‘N’ контролира реда на преминаване между честотната лента и ограничителната лента. Следователно по-висок ред, ускорете прехода, така че при n = ∞ филтърът на стойност масло се превръща в идеален високочестотен филтър.
По време на изпълнението на този филтър за простота ние разглеждаме ωc = 1 и решаваме трансферната функция
за s = jω, т.е. H (s) = s / (s + ωc) = s / (s + 1) за поръчка 1:
H (s) = s ^ 2 / (s ^ 2 + ∆ωs + (ωc ^ 2) за поръчка 2
Следователно трансферната функция на каскадата във високочестотния филтър е


Bode Парцел масло на стойност високочестотен филтър
Приложения на високочестотен филтър
Приложенията за високочестотни филтри включват основно следното.
- Тези филтри се използват в колоните за усилване.
- Високочестотен филтър се използва за премахване на нежелани звуци близо до долния край на звуковия обхват.
- За да се предотврати усилването на Постоянен ток които могат да навредят на усилвателя, за променливотоково свързване се използват високочестотни филтри.
- Високочестотен филтър Обработка на изображение : Високочестотни филтри се използват при обработка на изображения за изостряне на детайлите. Прилагайки тези филтри върху изображение, можем да преувеличим всяка малка част от детайлите в изображението. Но прекаляването може да повреди изображението, тъй като тези филтри усилват шума в изображението.
Все още има много разработки в дизайна на тези филтри, за да се постигнат стабилни и идеални резултати. Тези прости устройства играят важна роля в различни системи за контрол , автоматични системи, Обработка на изображения и аудио. Кое от приложението на Високочестотен филтър попадал ли си?