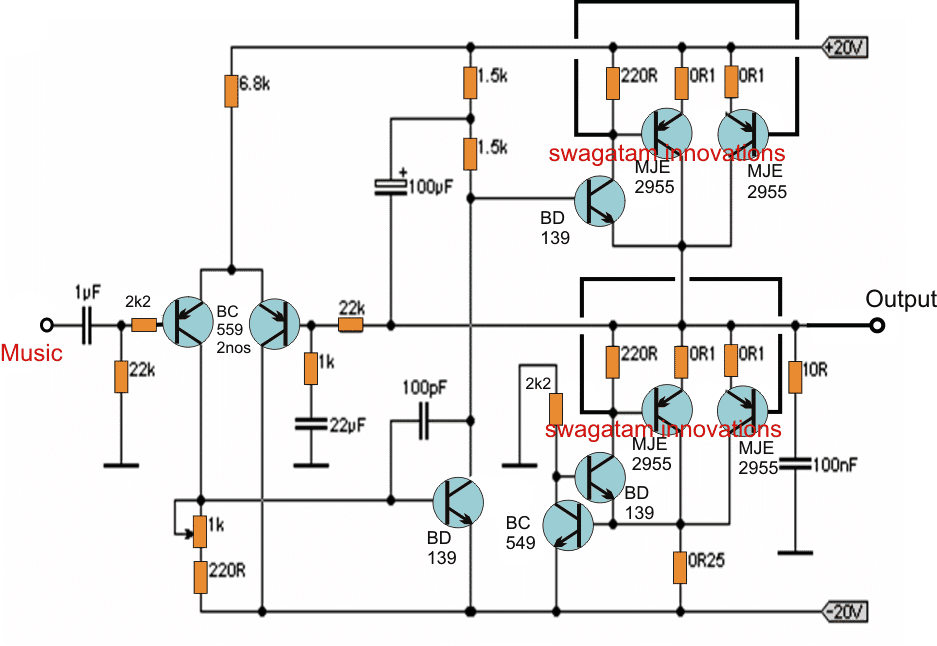
За всяка електрическа верига има две или допълнителни независими захранвания като ток, напрежение или и двата източника. За изследването им електрически вериги , теорема за суперпозицията е широко използван и най-вече за вериги с времева област на различни честоти. Например, линейна верига за постоянен ток се състои от едно или повече независими захранвания, ние можем да получим захранванията като напрежение и ток, като използваме методи като мрежов анализ и техники за възлов анализ. В противен случай можем да използваме „теоремата за суперпозицията“, която включва всеки индивидуален резултат от предлагането на стойността на променливата, която трябва да бъде решена. Това означава, че теоремата приема, че всяко захранване във верига открива независимо скоростта на променливата и накрая произвежда вторичната променлива чрез вмъкване на променливите, които са аргументирани от ефекта на всеки източник. Въпреки че процесът му е много труден, но все пак може да се приложи за всяка линейна верига.

Какво е теорема за суперпозицията?

Теоремата за суперпозицията е метод за независими доставки, налични в електрическа верига като напрежение и ток и това се счита за едно захранване наведнъж. Тази теорема казва, че при линейно n / w, съдържащо един или повече източници, потокът на ток през множество захранвания във верига е алгебричното изчисление на токовете, когато източниците действат независимо.

Приложението на тази теорема включва просто линейни n / ws, както и в AC и DC вериги, където помага за изграждането на вериги като ' Нортън ' както и ' Тевенин ”Еквивалентни схеми.

Например, веригата, която има две или повече захранвания, тогава веригата ще бъде разделена на няколко вериги въз основа на изявлението на теоремата за суперпозицията. Тук разделените вериги могат да направят цялата схема да изглежда много проста при по-лесни методи. И чрез сливане на разделените вериги друг път след индивидуална модификация на веригата, може просто да се открият фактори като напрежения на възлите, спадане на напрежението при всяко съпротивление, токове и т.н.

Стъпка по стъпка Методи за изложение на теоремата за суперпозицията

Следващите стъпка по стъпка методи се използват за откриване на реакцията на верига в конкретно разделение чрез теорема за суперпозицията.

Изчислете реакцията в специфичен клон на верига, като позволите едно независимо захранване, както и премахване на остатъчните независими захранвания тока в мрежата.
Направете отново горната стъпка за всички източници на напрежение и ток във веригата.
Включете всички реакции, за да получите общия отговор в определена верига, когато всички консумативи са в мрежата.

Какви са условията за прилагане на теоремата за суперпозицията?

Следните условия трябва да бъдат изпълнени, за да се приложи тази теорема към мрежа

Компонентите на веригата трябва да са линейни. Например, потокът на ток е пропорционален на напрежението на резисторите, което се прилага към веригата, поточната връзка може да бъде пропорционална на тока за индуктори.
Компонентите на веригата трябва да бъдат двустранни, което означава, че потокът на ток в противоположните полярности на източника на напрежение трябва да бъде еднакъв.
Компонентите, използвани в тази мрежа, са пасивни, тъй като не усилват иначе коригират. Тези компоненти са резистори, индуктори и кондензатори.
Активните компоненти не трябва да се използват, тъй като те рядко са линейни, както и никога двустранни. Тези компоненти включват основно транзистори, електронни тръби и полупроводникови диоди.

Примери за теорема за суперпозицията

Основната електрическа схема на теоремата за суперпозицията е показана по-долу и е най-добрият пример за тази теорема. Като използвате тази схема, изчислете потока на тока през резистора R за следната верига.

DC верига - Теорема за суперпозицията

Деактивирайте вторичния източник на напрежение, т.е. V2 и изчисляването на потока от ток I1 в следната схема.

Когато източникът на напрежение V2 е деактивиран

Знаем, че законът на ома V = IR

I1 = V1 / R

Деактивирайте първичния източник на напрежение, т.е. V1 и изчисляването на потока на ток I2 в следната схема.

Когато източникът на напрежение V1 е деактивиран

I2 = -V2 / R

Според теоремата за суперпозицията токът на мрежата I = I1 + I2

I = V1 / R-V2 / R

Как да използвам теоремата за суперпозицията?

Следващите стъпки ще ви кажат как да приложите теорема за суперпозицията за решаване на проблем.

Вземете един източник във веригата
Останалите независими източници трябва да бъдат настроени на нула чрез замяна на източници на напрежение чрез късо съединение, докато източниците на ток с отворена верига
Оставете независимите източници
Изчислете потока на текущата посока, както и величината в целия необходим клон като резултат от единичния източник, предпочитан в първата стъпка.
За всеки източник повторете стъпките от първата до четвъртата, докато необходимият ток на разклонение не бъде измерен, защото източникът действа сам.
За необходимия клон добавете всички текущи компоненти, като използвате указания. За веригата за променлив ток трябва да се направи фазовата сума.
Трябва да се следват същите стъпки за измерване на напрежението в който и да е елемент във веригата.

Задачи на теоремата за суперпозицията

Следващата схема показва основната верига за постоянен ток за решаване на проблема за теоремата за суперпозицията, така че да можем да получим напрежението на клемите на товара. В следващата схема има две независими захранвания, а именно ток и напрежение.

Обикновена схема на постоянен ток

Първоначално в горната верига поддържаме, че действа само захранването, а останалото захранване като тока се променя с вътрешно съпротивление. Така че горната схема ще се превърне в отворена верига, както е показано на фигурата по-долу.

Когато е активен един източник на напрежение

Помислете за напрежението на терминалите за натоварване VL1, като захранването се изпълнява самостоятелно

VL1 = Vs (R3 / (R3 + R1))

Тук Vs = 15, R3 = 10 и R2- = 15

Моля, заменете горните стойности в горното уравнение

VL1 = Vs × R3 / (R3 + R2)

= 15 (10 / (10 + 15))

15 (10/25)

= 6 волта

Задръжте само токовото захранване и променете захранващото напрежение с вътрешното му съпротивление. Така веригата ще се превърне в късо съединение, както е показано на следващата фигура.

Късо съединение

“проверка на кондензатор с мултицет ”

Помислете, че напрежението на клемите за натоварване е „VL2“, докато се изпълнява само токово захранване. Тогава

VL2 = I x R

IL = 1 x R1 / (R1 + R2)

R1 = 15 RL = 25

= 1 × 15 / (15 +25) = 0,375 ампера

VL2 = 0,375 × 10 = 3,75 волта

В резултат на това знаем, че теоремата за суперпозицията гласи, че напрежението върху товара е размерът на VL1 и VL2

VL = VL1 + VL2

6 + 3,75 = 9,75 волта

Предпоставки на теоремата за суперпозицията

Теоремата за суперпозицията, просто приложима за веригите, които могат да бъдат намалени към комбинации от последователни или паралелни за всеки източник на енергия в даден момент. Така че това не е приложимо за изследване на небалансирана мостова верига. Той просто работи навсякъде, където основните уравнения са линейни.
Изискването за линейност не е нищо друго, а е подходящо само да се определят напрежението и тока. Тази теорема не се използва за вериги, където съпротивлението на който и да е компонент варира в зависимост от текущото напрежение.

Следователно веригите, включващи компоненти като газоразрядни или лампи с нажежаема жичка, иначе варистори не могат да бъдат оценени. Друго изискване на тази теорема е компонентите, които се използват във веригата, да бъдат двустранни.

Тази теорема използва при изучаването на AC (променлив ток) вериги, както и полупроводникови вериги, където променливият ток често се смесва чрез постоянен ток. Тъй като променливото напрежение, както и уравненията на тока, е линейно подобно на постоянен ток. Така че тази теорема се използва за изследване на веригата с източник на постоянен ток, след това с източник на променлив ток. И двата резултата ще бъдат комбинирани, за да се каже какво ще се случи и с двата действащи източника.

Експеримент на теоремата за суперпозицията

Експериментът на теоремата за суперпозицията може да се направи по следния начин. Стъпка по стъпка на този експеримент е разгледана по-долу.

Целете се

Проверете експериментално теоремата за суперпозицията, като използвате следната схема. Това е аналитичен метод, използван за определяне на токове във верига, използващ повече от един източник на захранване.

Апаратура / необходими компоненти

Апаратите на тази схема са макет, свързващи проводници, милиамперметър, резистори и др.

Теория на експеримента

Теоремата за суперпозицията се използва просто, когато веригата включва два или повече източника. Тази теорема се използва главно за съкращаване на изчисленията на веригата. Тази теорема гласи, че в двустранна верига, ако се използват редица енергийни източници като два или повече, тогава потокът на ток ще бъде там във всяка точка и това е сумата от всички токове.

Потокът ще бъде в точката, където всеки източник е бил разгледан поотделно, а други източници ще бъдат променени по това време чрез импеданс, който е еквивалентен на техните вътрешни импеданси.

Електрическа схема

Експериментална схема на теоремата за суперпозицията

Процедура

Поетапната процедура на този експеримент е разгледана по-долу.

Свържете DC захранване през клемите на 1 и I1 & приложеното напрежение е V1 = 8V и по същия начин се прилага към клемите, където захранването V2 е 10 волта
Измерете потока на тока във всички разклонения и те са I1, I2 & I3.
Първо свържете източника на напрежение V1 = 8V през клемите от 1 до I1, а терминалите за късо съединение през 2 до I2 е V2 = 0V.
Изчислете потока на токове във всички разклонения за V1 = 8V и V2 = 10V през милиамперметър. Тези токове са означени с I1 ’, I2’ & I3 ’.
По същия начин свържете единствените V2 = 10 волта през 2 към I2 клеми, както и терминали за късо съединение 1 и I1, V1 = 0. С помощта на милиамперметър се изчислява потокът на тока във всички разклонения за двете напрежения и те се означават с I1 ”, I2” & I3 ”.

За да проверите теоремата за суперпозицията,

I1 = I1 ’+ I1”

I2 = I2 ’+ I2’

I3 = I3 ’+ I3”

Измерете теоретичните стойности на токовете и те трябва да бъдат еквивалентни на стойностите, които се измерват за токове.

Таблица за наблюдение

Стойностите на I1, I2, I3, когато V1 = 8V & V2 = 10V, стойностите на I1 ', I2' & I3 ', когато V1 = 8V и V2 = 0 и за стойностите, I1', I2 '& I3 ', когато V1 = 0 и V2 = 10V.

V1 = 8V V2 = 10V	V1 = 8V V2 = 0V	V1 = 0V V2 = 10V
I1	I1 '	I1 ''
I2	I2 ’	I2 ’’
I3	I3 ’	I3 ’’

Окончателна експериментална схема на теоремата за суперпозицията

Заключение

В горния експеримент разклоненият ток не е нищо друго освен алгебричната сума на токовете поради отделния източник на напрежение, след като останалите източници на напрежение са късо съединение, поради което тази теорема е доказана.

Ограничения

Ограниченията на теоремата за суперпозицията включват следното.

Тази теорема не е приложима за измерване на мощност, но измерва напрежението и тока
Използва се в линейни вериги, но не се използва в нелинейни
Тази теорема се прилага, когато веригата трябва да има над един източник
За небалансирани мостови вериги той не е приложим
Тази теорема не се използва за изчисления на мощността, тъй като работата на тази теорема може да се извърши въз основа на линейността. Тъй като уравнението на мощността е произведение на ток и напрежение, иначе квадрат на напрежението или тока, но не линейно. Следователно мощността, използвана през елемента във верига, използвайки тази теорема, не е постижима.
Ако опцията за натоварване е променлива, в противен случай съпротивлението на натоварването варира редовно, тогава е необходимо да се постигне всеки принос на източника за напрежение или ток и тяхната сума за всяко преобразуване в рамките на съпротивлението на натоварване. Така че това е много труден процес за анализ на трудни вериги.
Теоремата за суперпозицията не може да бъде полезна за изчисления на мощността, но тази теорема работи на принципа на линейността. Тъй като уравнението на мощността не е линейно. В резултат на това мощността, използвана от фактора във верига с тази теорема, не е постижима.
Ако изборът на натоварване е променлив, тогава е необходимо да се постигне всяко дарение на захранване и тяхното изчисление за всяко преобразуване в съпротивление на натоварване. Това е много труден метод за анализ на съставни вериги.

Приложения

The приложение на теоремата за суперпозицията е, можем да използваме само линейни вериги, както и веригата, която има повече запаси.

От горните примери за теорема за суперпозиция, тази теорема не може да се използва за нелинейни вериги, но е приложима за линейни вериги. Веригата може да бъде изследвана с един източник на захранване наведнъж,

“електроинженер висши дизайнерски идеи ”

Еквивалентните секционни токове и напрежения включват алгебрично откриване на това, което ще изпълняват при всяко захранване в сила. За да отмените всички проучвания с изключение на едно захранване, заменете всеки източник на захранване с кабел, възстановете всяко текущо захранване с прекъсването.

По този начин става въпрос за всичко преглед на теоремата за суперпозицията което гласи, че като използваме тази теорема, в даден момент можем да анализираме веригата, използвайки само един източник на захранване, свързаните компонентни токове, както и напреженията, могат да се добавят алгебрично, за да се наблюдава какво ще постигнат, използвайки ефективно всички източници на енергия. За да отмените всички, но един източник на енергия за анализ, след това сменете всеки източник на напрежение с проводник и променете всеки източник на ток чрез отворен (прекъсване). Ето въпрос към вас, какво е KVL?