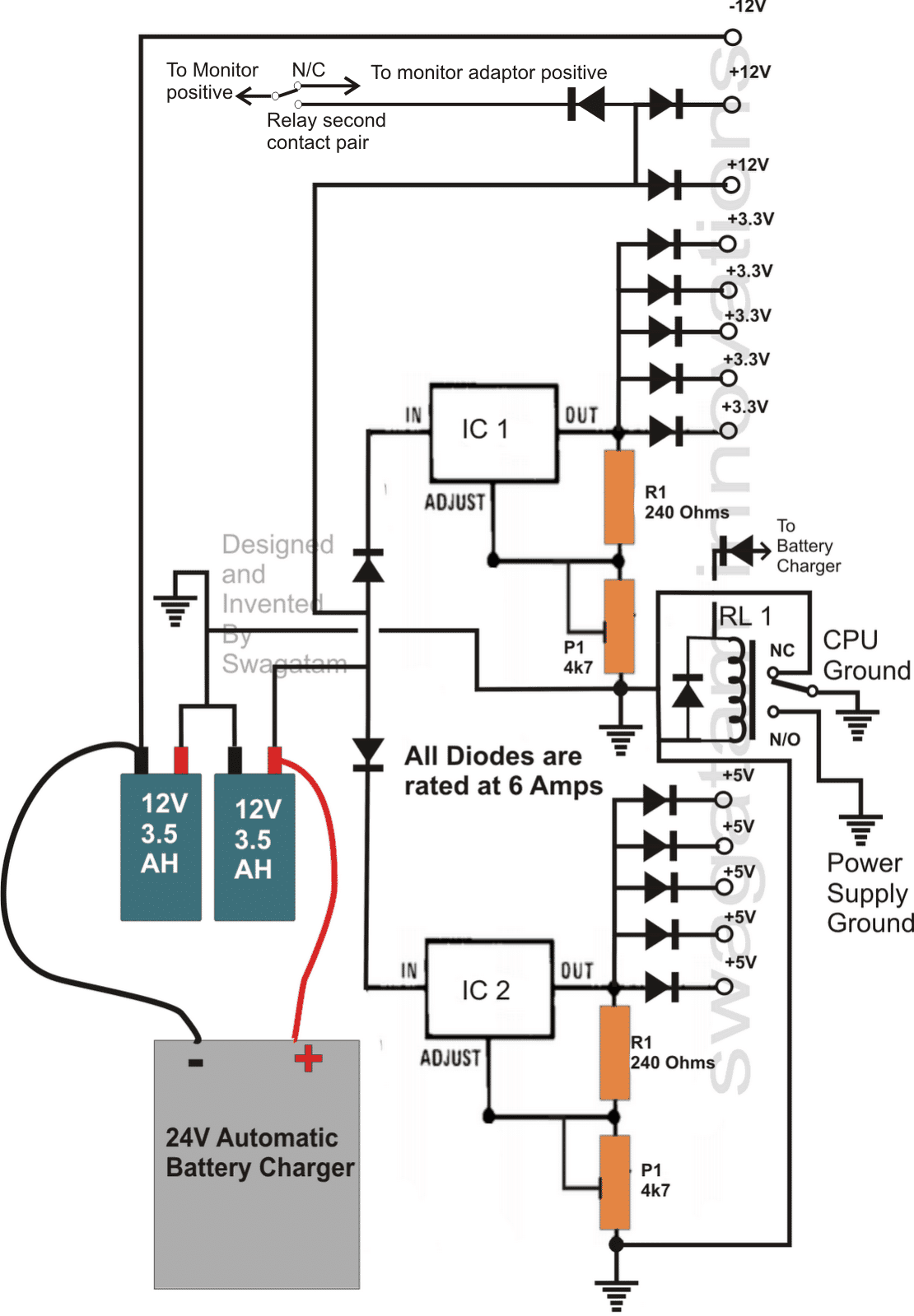
В транзисторите характеристиките на трансфер могат да се разберат като начертаване на изходен ток спрямо входяща контролна величина, което следователно показва директен „трансфер“ на променливи от вход към изход в кривата, представена на графиката.
Знаем, че за биполярен преходен транзистор (BJT) изходният ток на колектора IC и контролния входен ток IB са свързани с параметъра бета , което се приема за постоянно за анализ.
Позовавайки се на уравнението по-долу, намираме линейна връзка, съществуваща между IC и IB. Ако направим IB ниво 2x, тогава IC също се удвоява пропорционално.

Но за съжаление, тази удобна линейна връзка може да не е постижима в JFET за техните входни и изходни величини. По-скоро връзката между ID на тока на източване и VGS напрежение на затвора се определя от Уравнение на Шокли :

Тук квадратният израз става отговорен за нелинейния отговор в ID и VGS, което поражда крива, нарастваща експоненциално, тъй като величината на VGS намалява.
Въпреки че математическият подход би бил по-лесен за прилагане за постояннотоков анализ, графичният начин може да изисква начертаване на горното уравнение.
Това може да представи въпросното устройство и начертаването на мрежовите уравнения, свързани с идентичните променливи.
Намираме решението, като гледаме точката на пресичане на двете криви.
Не забравяйте, че когато използвате графичен метод, характеристиките на устройството остават незасегнати от мрежата, където устройството е внедрено.
Тъй като пресечната точка между двете криви се променя, това също променя уравнението на мрежата, но това не оказва влияние върху трансферната крива, определена от горното уравнение, 5.3.
Следователно като цяло можем да кажем, че:
Характеристиката за прехвърляне, определена от уравнението на Шокли, не се влияе от мрежата, в която е внедрено устройството.
Можем да получим трансферната крива, използвайки уравнението на Шокли или от изходните характеристики както е показано на фиг. 5.10
На фигурата по-долу можем да видим две графики. Вертикалната линия измерва милиампера за двете графики.

Едната графика изобразява идентификационния ток на източващия ток спрямо напрежението VDS от източника към източника, втората графика изобразява тока на източване спрямо напрежението от източника към източника или ID срещу VGS.
С помощта на характеристиките на изтичане, показани в дясната страна на оста „y“, ние можем да начертаем хоризонтална линия, започваща в областта на насищане на кривата, показана като VGS = 0 V до оста, показана като ID.
Понастоящем постигнатите нива за двете графики са IDSS.
Точката на пресичане на кривата на ID срещу VGS ще бъде дадена по-долу, тъй като вертикалната ос е дефинирана като VGS = 0 V

Обърнете внимание, че характеристиките на изтичане показват връзката между една изходна величина на изтичане с друга изходна величина на изтичане, при което двете оси се интерпретират от променливи в една и съща област на характеристиките на MOSFET.
По този начин, трансферните характеристики могат да бъдат дефинирани като график на изтичащ ток на MOSFET спрямо количество или сигнал, действащ като входно управление.
Следователно това води до директен „трансфер“ през входно / изходни променливи, когато кривата се използва вляво на Фигура 5.15. Ако беше линейна връзка, графиката на ID срещу VGS щеше да бъде права линия през IDSS и VP.
Това обаче води до параболична крива поради вертикалното разстояние между VGS, преминаващо през характеристиките на изтичане, което намалява в значителна степен, тъй като VGS става все по-отрицателна, на фиг. 5.15.
Ако сравним пространството между VGS = 0 V и VGS = -1V с това между VS = -3 V и откъсването, виждаме, че разликата е идентична, въпреки че е много по-различна за стойността на ID.
Ние можем да идентифицираме друга точка на трансферната крива, като изчертаем хоризонтална линия от VGS = -1 V крива до оста на ID и впоследствие я разширим до другата ос.
Обърнете внимание, че VGS = - 1V в долната ос на трансферната крива, когато ID = 4,5 mA.
Също така имайте предвид, че в дефиницията на ID при VGS = 0 V и -1 V се използват нивата на насищане на ID, докато омичната област се пренебрегва.
Продължавайки напред, с VGS = -2 V и - 3V, ние можем да завършим графиката на трансферната крива.
Как да приложим уравнението на Шокли
Можете също така директно да постигнете кривата на прехвърляне на фиг. 5.15, като приложите уравнението на Шокли (уравнение 5.3), при условие че са дадени стойностите на IDSS и Vp.
Нивата IDSS и VP определят границите на кривата за двете оси и изисква само начертаване на няколко междинни точки.
Истинността на Уравнение на Шокли Уравнение 5.3 като източник на трансферната крива от фигура 5.15 може да бъде перфектно изразено чрез инспектиране на определени отличителни нива на определена променлива и след това идентифициране на съответното ниво на другата променлива по следния начин:


Това съответства на графиката, показана на фиг. 5.15.
Наблюдавайте колко внимателно се управляват отрицателните знаци за VGS и VP при горните изчисления. Пропускането дори на един отрицателен знак може да доведе до напълно грешен резултат.
От горната дискусия става съвсем ясно, че ако имаме стойностите на IDSS и VP (които могат да бъдат препратени от листа с данни), можем бързо да определим стойността на ID за всяка величина на VGS.
От друга страна, чрез стандартната алгебра можем да извлечем уравнение (чрез уравнение 5.3) за полученото ниво на VGS за дадено ниво на идентификатор.
Това може да се извлече съвсем просто, за да се получи:

Сега нека проверим горното уравнение, като определим нивото на VGS, което произвежда изтичащ ток от 4,5 mA за MOSFET, имащ характеристиките, съответстващи на фиг. 5.15.

Резултатът потвърждава уравнението, както е в съответствие с фиг. 5.15.
Използване на метода на стенографията
Тъй като трябва да начертаем кривата на прехвърляне доста често, може да се окаже удобно да получим стенографска техника за нанасяне на кривата. Желан метод би бил, който позволява на потребителя да начертае кривата бързо и ефективно, без да се прави компромис с точността.
Уравнението 5.3, което научихме по-горе, е проектирано така, че определени нива на VGS дават нива на ID, които могат да бъдат запомнени за използване като графични точки, докато се чертае кривата на прехвърляне. Ако посочим VGS като 1/2 от стойността за откъсване VP, полученото ниво на идентификатор може да бъде определено с помощта на уравнението на Шокли по следния начин:


Трябва да се отбележи, че горното уравнение не е създадено за конкретно ниво на VP. Уравнението е обща форма за всички нива на VP, стига VGS = VP / 2. Резултатът от уравнението предполага, че източният ток ще бъде винаги 1/4 от нивото на насищане IDSS, стига напрежението от порта към източника да е с 50% по-малко от стойността на откъсването.
Моля, обърнете внимание, че нивото на идентификатор за VGS = VP / 2 = -4V / 2 = -2V съгласно фиг. 5.15
Избирайки ID = IDSS / 2 и го замествайки в уравнение 5.6, получаваме следните резултати:

Въпреки че могат да се установят допълнителни брой точки, достатъчно ниво на точност може просто да се постигне чрез изчертаване на кривата на прехвърляне, като се използват само 4 точки на графиката, както е посочено по-горе и също в Таблица 5.1 по-долу.
В повечето случаи можем да използваме само точката на графиката, използвайки VGS = VP / 2, докато пресичанията на оста при IDSS и VP ще ни дадат крива, достатъчно надеждна за по-голямата част от анализа.

Предишен: MOSFET - тип подобрение, тип изчерпване Напред: Разбиране на процеса на включване на MOSFET