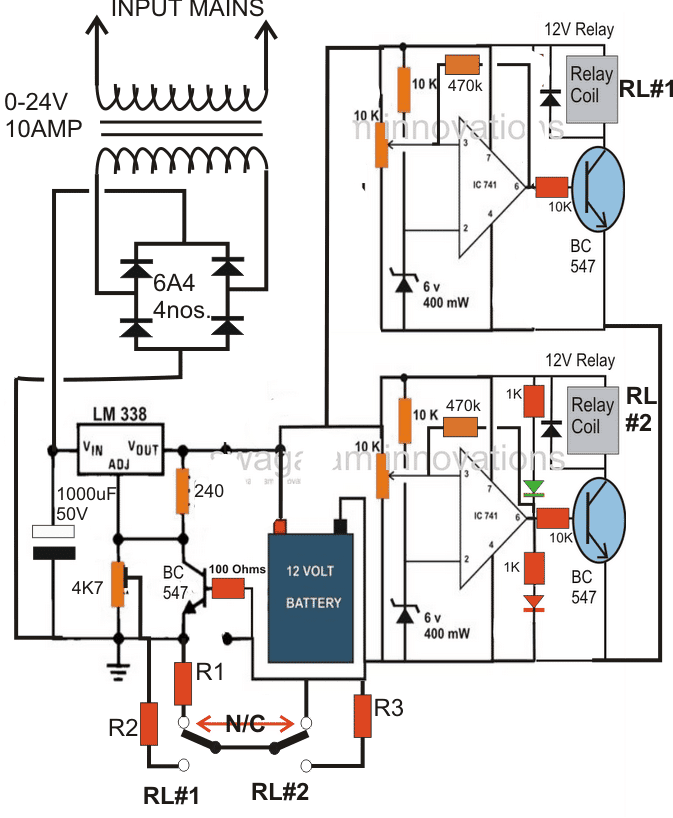
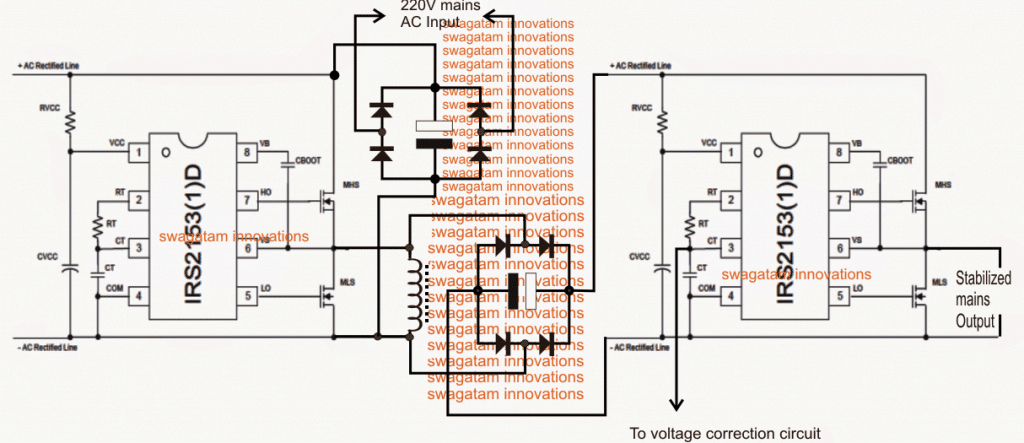
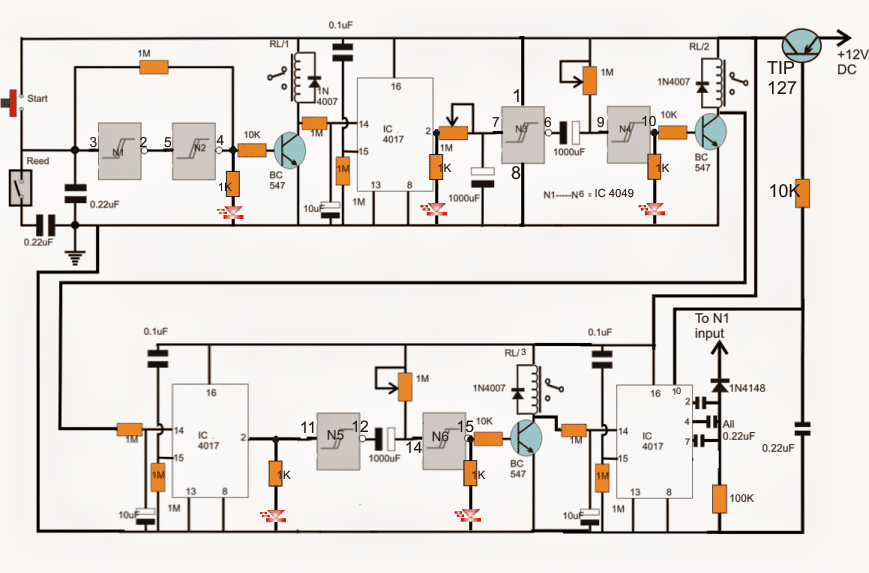
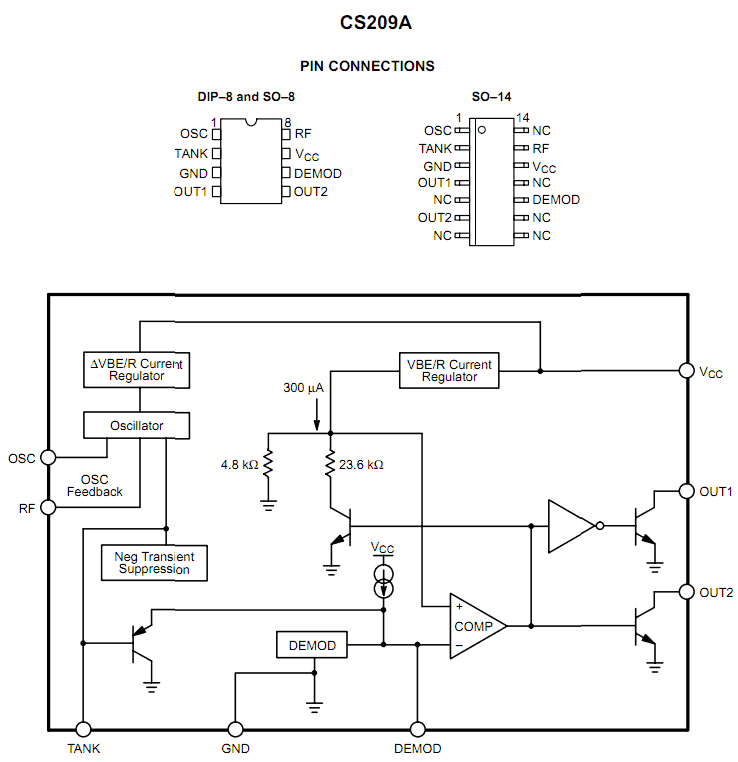
Корените на двоичната бройна система се крият в китайската литература. Съвременната двоична система е измислена от Готфрид Лайбниц през 1689 г. Неговата теология се основава на християнската идея за „Сътворение от нищо“. Той се опитваше да намери система, която да преобразува словесните твърдения на логиката в математически. В класическия китайски текст 'Книга на промените' той открива двоичен код това потвърди теорията му, че животът може да бъде сведен до серия от директни пропорции. След това той създаде система, която може да представи информацията под формата на редове от нула и единици. Използването на двоичната система може да се намери в древен текст преди 16 век. Преди 1450 г. жителите на остров Мангарева във Френска Полинезия са използвали хибридна двоично-десетична система. Двоично-десетични преобразувания са описани в тази статия.
Какво е двоична бройна система?
Използването на двоични числа може да се намери в текстовете на древни култури като Египет, Китай и Индия. В тази система текстът, данните и числата са представени като числово число base-2, което използва само два символа. В тази система числата са представени като редовете на 0 и 1. Всяка цифра се нарича „бит“. Колекцията от 4-битови е известна като „Nibble“ и 8-битовите образуват „Byte“.
Какво представлява десетичната бройна система?
Десетичните числа са известни още като индуистко-арабски числа. Това е позиционна бройна система. Нарича се още система base-10, тъй като използва 10 символа за представяне на числовото. символи 0, 1, 2, 3, 4, 5, 6, 7, 8 и 9 се използват в тази система. Символът „0“ е изобретен в Индия и идеята е пренесена на изток от араби по време на търговия. По този начин тази система е известна в народите като индуистко-арабска система. Използването на тази система в западната култура е започнало през 12 век в търговията и науките.
Използване на двоична бройна система
През 1847 г. Джордж Бул в своя доклад „Математическият анализ на логиката“ описва булева алгебра. Тази система се основава на двоична логика ON-OFF. Клод Шанън забеляза сходството между булевата алгебра и логиката на електрически вериги . През 1937 г. Шанън публикува своите открития в дипломната си работа, която се превърна в начална точка от мястото, където бинарната система се използва в цифровата логика, компютрите, електрическите вериги и т.н ...
Всички съвременни компютри използват двоично кодиране за своя набор от инструкции и съхранение на данни. Цифровите данни се съхраняват под формата на двоични битове. Дигитален безжична комуникация прехвърля данни под формата на двоични битове.
Десетичен в двоичен метод на преобразуване
Използваме десетични числа в ежедневните си изчисления и номериране. Но машини като компютри и електронно оборудване използват двоични файлове и могат да разберат само двоичните данни. Така че, важно е да преобразувате десетичните числа в двоични числа.
За да конвертирате десетично число в двоично, разделете числото с 2. Напишете резултата отдолу и остатъка от дясната страна. Ако няма остатък, напишете 0. Разделете резултата с 2 и продължете горния процес. Повторете процеса, докато резултатът стане ‘0’. Прочетете остатъците отдолу нагоре, това дава двоичен еквивалент на даденото десетично число. MSB е най-долният остатък, докато първият остатък образува LSB на двоичното число.
Пример за преобразуване в десетично в двоично
Нека разгледаме един пример, за да разберем метода на десетичното в двоично преобразуване. Десетичните числа са представени с основа 10, докато двоичните числа са представени с основа 2.
Най-десният бит от двоичното число е известен като Най-малко значимият бит, а най-левият бит е известен като Най-значимият бит.

Десетично в двоично преобразуване
В горния пример е дадено двоично преобразуване на десетичното число 65. Стрелката нагоре показва реда, в който остатъците трябва да бъдат записани.
Метод на двоично в десетично преобразуване
Десетично число е известно още като числото Base-10. Това е позиционна система за номериране, така че трябва да се знае мястото на цифрите. Започвайки от дясната страна, стойностите на местата в десетичната бройна система са степента на 10. Например, за 1345 - Стойността на мястото на 5 е 100т.е. 1, Стойността на мястото на 4 е 101което е десетото място. По същия начин следващите стойности на място са 100, 1000 и т.н. ...
И така, даденото число може да се декодира като
(1 × 1000) + (3 × 100) + (4 × 10) + (5 × 1) = 1345.
Двоичната бройна система също е a позиционна система за номериране . Тук основата е 2. И така, степента на 2 се използва за намиране на стойностите на мястото. По този начин, за да преобразувате двоично число в десетично число, двоичните цифри трябва да се умножат със степента 2 и да се добавят.

Таблица за преобразуване в двоично в десетично число
Пример за преобразуване в двоично в десетично
За да разберете преобразуването, нека разгледаме пример. Нека преобразуваме 1101двев десетично число.
Започвайки от LSB, 1101две= (1 × 23) + (1 × 2две) + (0 × 21) + (1 × 20)
= (1 × 8) + (1 × 4) + (0 × 2) + (1 × 1):
= 8 + 4 + 0 + 1:
= 1310
По този начин десетичното представяне на 1101 е 13.
Десетичен на двоичен кодер
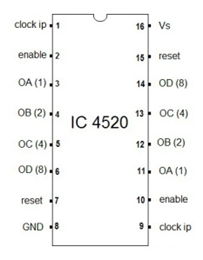
Енкодери се използват като преобразуватели на код в компютърни системи. Те се предлагат като интегрални схеми на пазара. За преобразуване на десетично число в двоично се използва десетичен в BCD енкодер. В системата BCD десетичното число е представено като четирицифрено двоично число. Той може да преобразува десетичните числа от 0 до 9 в двоичен поток.
Кодерът е a комбинационна логическа схема . Реверсът на кодера е декодер, който извършва обратното действие. Таблицата на истината на десетичния към BCD кодера е дадена по-долу.

Десетична към двоична кодираща таблица на истината
От таблицата на истината по-горе оформете уравненията за думите A3, A2, A1, A0. Следователно логическите уравнения са както по-долу -
A3 = 8+9: A2 = 4+5+6+7 : A1 =2+3+6+7 : A0= 1+3+5+7+9
Сега, разглеждайки логическите уравнения по-горе, оформете комбинационната верига с ИЛИ порти.

Десетичен към двоичен кодер
Цифровите технологии заменят аналоговите методи в много области на науката, комуникацията и търговията. Различната точна и достъпна потребителска електроника също се увеличава. Всички тези системи приемат входни данни в различни форми и представяния като азбуки, десетични, шестнадесетични и др. Но вътрешно всички данни се обработват и съхраняват под формата на двоични числа и битове. По този начин за компютърния програмист и разработчик е важно да се знае връзката на всички тези различни видове данни с двоичната система за номериране. Проверете разбирането си за двоичното преобразуване, като преобразувате десетичното число 45 в неговия двоичен еквивалент.